 文章内容
文章内容
科里奥利质量流量计动态特性的研究
引言测量原理概述 测量管的振动分析有限元模态分析支承类型对模态频率的影晌
摘要 应用有限元模态分析方法,对科里奥利质量流量计(CMF)单直管简化模型进行了模态分析。这了考察CMF套管和支承管等对模态的影响,对单直管CMF整体模型,依据其轴对称结构特点,利用现成的二维CAD视图,导入到Marc中旋转生成三维模型,进行模态分析。采用Lanczos法求解模态。最后研究了支承类型对测量管模态的影响,计算结果表明,边界条件不同,模态频率变化很大。
关键词 科里奥利质量流量计 动态特性 有限元模态分析
科里奥利质量流量计(CMF)是一种用于直接测量质量流量的流量计,它在原理上消除了温度、压力、流体状态、密度等参数的变化对测量精度的影响,可以适应气体、液体、两相流、高粘度流体和糊状介质的测量,是一种高精度的适应范围很广的测量方法,它还具有压力损失小、自排空、保持清洁等众多特点,是流量测量的发展方向之一。
科里奥利质量流量计,是利用流体流过振动管道时产生科里奥利效应对管道两端振动相位的影响来测量流过管道的流体质量的。要深人了解CMF的工作情况并改进CMF的性能,有必要研究CMF的振动模态。其作用有:
①为了容易激振,一般都选择测量管的谐振频率作为激振频率;
②选择合适的激振频率避开工业现场的干扰,会给信号分离带来便利;
③激振器、拾振器和电路的设计及信号的处理都需要了解振动频率;
④拾振器的布置需要了解CMF的模态;
⑤结构优化,应力、应变以及疲劳寿命的计算;
⑥可以利用CMF系统中的振动信号进行状态监测和故障预报;
⑦了解振动的过程,得到偏离理想振动下的误差以及补偿;
⑧了解干扰振动带来的误差,采取措施来消除或防止系统可能出现的干扰振动,从而确保CMF的精度和可靠性心
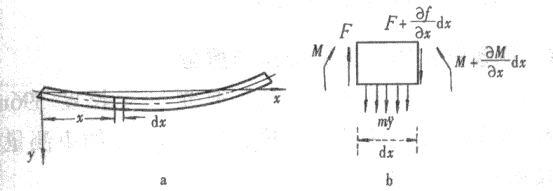
科里奥利流量计有多种形式,下面以单直管科里奥利流量计为例来讨论。如图l所示,测量管的中间设置有激振装置,两端设置有拾振传感器。没有流体流过的时候,管子的振动如图la所示,管子两端的振动状态相同。当流体流过振动管道时,就产生和激振频率相同的科里奥利加速度和科里奥利力,如图lb所示,AC段和CB段的科里奥利力大小相同,方向相反,作用叠加在测量管上,便管子产生了扭曲和振动相位变化。科里奥利力和流过管道的流体密度和流速成正比(即质量流量)。对于线性系统,可知质量流量却相位差成正比。
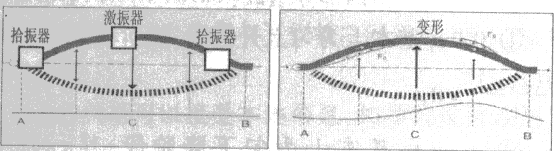
图l 质量流量计测量原理 管道中流体的科里奥利加速度为 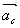 =2
=2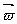 ×
× 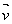 ,流体微元所受到的科里奥利力dFc=-dm ·
,流体微元所受到的科里奥利力dFc=-dm · 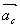 =2
=2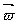 ×
×  ·dm。入口段和出口段的瞬时振动角速度方向相反。可见入口段科里奥利力与振动方向相反,使振动减弱和滞后;出口段科里奥利力巧振动方向相同,使振动加强和提前。
·dm。入口段和出口段的瞬时振动角速度方向相反。可见入口段科里奥利力与振动方向相反,使振动减弱和滞后;出口段科里奥利力巧振动方向相同,使振动加强和提前。
根据两端固定支承梁的振动方程和所受的科里奥利力,可以得出两侧检测点的振动信号相位差和质量流量成正比的结论:
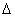
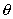 =(K / E)qm
=(K / E)qm
式中:K为常数;E为弹性模量;qm为质量流量。
如图2所示,是单直管科氏质量流量计的一种方案,由测量管、支承管、套管、电磁激振器、拾振器(电磁振动传感器)和联接法兰等组成。

测量管两端和套管的联结一般采用焊接或者胶接,中部受激振力,细长结构,所以可以简化为梁模型。两端近似刚性支承,可以简化为固支梁。
梁段的弯曲转动效应与剪切变形略去不计,若引用牛顿力学来建立梁弯曲振动时的运动方程,可由梁中截取一微元段,梁在对称平面内作铅垂方向振动时,微元主要作上下运动。图3a表示在梁在x一y平面内振动。静止时y(x,0)=0。在某种激励下梁离开了平衡位置。从梁的任意截面x取出一小段dx,它的受力见图3b。这一小段的质量为m,上下振动的加速度为  y /
y / 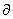 t2。由微元段的平衡条件得到:
t2。由微元段的平衡条件得到:
- 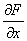 =m
=m 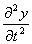 ;
;  =F
(1)
=F
(1)
式中:F为剪力;M为弯矩;m为梁单位长度的质量;y为梁弯曲振动时的挠曲位移。
略去剪切变形对梁的挠曲位移的影响时,有
M=EIx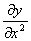
式中:EIx为梁的抗弯刚度。用挠度y表示的梁的弯曲振动的运动微分方程:
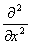 (EIx
(EIx 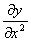 )+m
)+m  =0
(2)
=0
(2)
对于具有边界条件的梁,运动方程式(2)可用分离变量法求解,为此设
y(t,x)=W(x)T(t) (3)式中:T(t)代表每一点的运动规律,比如正弦振动;W(x)为x点的幅度,表示了横向振动幅度沿着测量管轴向的分布。梁作弯曲振动时,解为
T(t)=Asin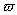 t+Bcos
t+Bcos 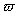 t
(4)
t
(4)
对于等剖面的均匀梁,由式(2)也得(EIxW’’)- 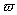 2mW=0,记a2=EIx / m,记
2mW=0,记a2=EIx / m,记 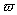 2 / a2=k4(即k=
2 / a2=k4(即k=  )因而有微分方程:
)因而有微分方程:
 (4)-k4W=0
(5)
(4)-k4W=0
(5)
通解形式为W(x)=A ,代人式(5)得其特征方程
,代人式(5)得其特征方程 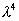 -k4=0,特征根
-k4=0,特征根  =k,-k,jk,-jk(j为单位虚数)。因此,式(5)的一般解为
=k,-k,jk,-jk(j为单位虚数)。因此,式(5)的一般解为
式中:C,D,E及F由边界条件决定。测量管一般是焊接到系统中的。所以边界条件为固支,有:
x=0 时,Y(0,t)=0,即W(0)=0;Y’(0,t)=0,即W’(0)=0; x=L时,Y(L,t)=0,即W(L)=0;Y’(L,t)=0,即W’(L)=0;解方程可得测量管的各阶固有频率:
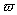 i=
i= 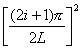
 (7)
(7)
CMF工作中,主要是要求测量管振动来实现对流量的测量,简单一点是只考虑测量管的振动,认为它是固定在CMF中的;全面一点考虑,应该考虑对CMF整体建模,主要部件都应该加入模型。
实际中,测量管两端并非刚性支承,如果要考虑套管等各个部件的振动,精确的理论模型会很复杂,一般只能采用有限元等数值计算方法来分析。本文中将对CMF做些简化,暂不考虑激振器和拾振器的附加质量的影响,也未考虑流固耦合的影响。采用MSC·Marc建立CMF的有限元模型。
3 CAD几何模型和CAE模型的建立
CMF为轴对称结构,可以采用二维有限元模型,这里为了提高分析精度,采用了实体模型。
仅分析测量管时,由于其结构简单,所以可直接在Marc中方便地建立实体模型。如果要分析CMF整体的振动情况,需要对CMF整体建立实体模型。结构较复杂,Marc中建模较麻烦,可以利用CAD软件建立模型。CMF为轴对称结构,采用二维CAD模型在Marc中旋转产生三维CAD模型的建模方法。
①绘图:在AutoCAD中以1:1的尺寸比例,绘制二维装配图(平面视图)。省略或删除一些对模态分析影响不大的细节结构。按各零件的材料属性和联接关系,进行适当合并简化。
②导入几何模型:Marc的前后处理用户界面Mentat具有多种CAD格式数据文件接□,故由此可读入AutoCAD的DWG格式的二维模型,这样既节省建模时间,又避免了重复建模可能引起的差错。
③几何检查:检查每个区域是否由封闭曲线包围,消除曲线间的小间隙,合并删除过短曲线。焊接部位按照固联处理,法兰联接简化为固支。
④对各零件的平面区域分别划分网络:设种子点,自动划分有限元网格,对局部不合理的畸形单元进行适当手工调整,对于重合节点进行合并操作,保证相交面的交线处网格匹配。将对应于不同零件的区域内单元的全体,定义为不同的单元集合(element set),以便后面对不同(零件)区域的单元进行不同的操作。单元集合的定义方法是选择某个零件区域,分别执行单元存储操作,取合适的单元集名,就可存为不同的单元集合。命名尽量遵循见名知意的原则。
⑤旋转生成实体:将整个二维网格绕其对称轴旋转,就生成三维网格。平面单元的材料和几何属性也就自动赋给相应的三维单元。
在二维有限元分析中常用三角形和四边形单元,三角形单元对分析区域的边界逼近得较好,但变形性能不好,各边上的应变值是常数,会出现所谓单元"变硬"的现象,分析精度下降。为此,图4所示平面模型多采用四边形单元。

图4 CMF整体的二维平面网格图
旋转后的三维单元是Marc中的7号单元,为八节点六面体等参单元。采用假定应变法,提高低阶单元的弯曲变形。
⑥合并区域邻接处的冗余节点:测量管、套管和法兰之间为刚性联结,故即将各零件区域相邻处的重复节点合并;支承管和法兰之间采朋粘接。
⑦施加边界条件:流量计是通过法兰联接安装到管线上的。将法兰的螺栓联接简化为固定法兰外侧面,忽略螺栓孔,即限制法兰外侧面上每个节点的全部6个自由度。
对于单独测量管模型,有两端固支、一端仅可轴向自由移动、悬臂(一端完全自由)等。固支简化为管端面固定,约束端面节点的全部自由度;轴向自由是指沿着测量管轴线方向的移动自由度不限制;悬臂端,则没有约束,完全自由。
本例中CMF装配图,其划分后的二维平面网格如图4所示。Marc中旋转生成的整个流量计的实体模型,有限元网格如图5所示。

3.2 有限元计算方法的选择
模态求解,就是求解系统特征方程,方法主要有逆幂法和Lanczos法。当系统特征方程有两个特征值很接近时,逆幂法可以得到满意的结果;但如果有多于两个特征值很接近,则收敛性较差。另外,逆幂法仅对提取少数几阶模态特别有效。
Lanczos法将特征值问题转化为三对角矩阵的特征值问题,此法可用于确定所有模态或部分模态。由于本文所分析的流量计是轴对称结构,特征值一般会成对出现,采用逆幂法可能会出现求解过程无法收敛的问题,所以采用Lanczos法。
计算自由状态的模态,受自由边界条件的影响,刚度矩阵是半正定的,会出现刚体模态。必须允许非正定矩阵才能进行计算,矩阵的非正定经过反复迭代会带来很大误差,使模态计算结果失真。根据刚体模态全是0频的特点,设置模态计算的最低频率大于0,滤去0频率的影响,可以得到较好的计算结果。
4 有限元计算实例和分析
4·1测量管实体模型的模态与振型
建立测量管的实体模型,取测量管长度396mm(CMF整体长度除去法兰长度),壁厚1mm,约束测量管两端所有节点的自由度。计算测量管模态,可以发现对于每一频率,都有两个模态,弯曲振动方向相互垂直,与测量管的轴对称特征相吻合。相同频率的两个模态可以认为是同一阶模态,与欧拉梁理论模型的计算结果吻合。前四阶模态如图6所示。

图6 单独的测量管模型计算所得测量管模态
一股选样测量管的一阶模态频率作为CMF的激振频率,这样振幅大,有利于激振。也有利用高阶模态或者检测一阶模态的高次谐波,有利于避开工业现场强的低频干扰振动和噪声。4·2 CMF整体模型的模态与振型
图7a~图7d分别是CMF整体有限元模型的4阶模态、套管弯曲、支承管和测量管弯曲、整体(三层管)扭转、支承管弯曲等。为了便于查看,放大了变形,所以有时候会出现内层管穿出来了,并不表示真的如此,实际中的变形是非常微小的。

图7 CMF整体的模态
4.3 对比CMF整体有限元模型和单独的测量管固支模型
CMF整体模态与测量管模态是一致的。整体模态中一、三、阶模态就与测量管的一、二阶模态对应,表现为测量管的一、二阶弯曲,而且频率相差在0.3%以内。CMF整体模态中也出现了反映套管和支承振动的模态,所以流量计在设计过程中也应考虑支承管和套管对测量管的影响。
计算分析可以看出,只研究测量管低频动态特性时,由于法兰部分刚度较大,支承管和套管相对测量管刚度也较大,CMF中测量管的动态分析,可以根据具体情况,简化为除去法兰长度部分的测量管的分析,又由于其结构细长还可以按梁式模型简化。
表1 列出了前几阶模态。
表1 模态计算结果的比较
模态频率/Hz |
振型描述 |
|||
阶次 |
CMF整体模型 |
阶次 |
测量管模型 |
|
1 |
445.414 |
1 |
446.52 |
测量管一阶弯曲 |
2 |
1082.14 |
套管和支承管一阶弯曲 |
||
3 |
1216.75 |
2 |
1215.16 |
测量管二阶弯曲 |
4 |
1223.24 |
整体的扭转 |
||
5 |
1461.17 |
支承管一阶弯曲 |
||
3 |
2344.22 |
测量管三阶弯曲 |
||
4 |
3801.64 |
测量管四阶弯曲 |
||
前述两端固支类型的单直管科里奥利质量流量计中,轴向温度应力和残余应力的影响较大,所以流量计的温漂和随时间的漂移较大,另外由于弯曲刚度大,所以流量计的灵敏度低,相对环境干扰较大,就是信噪比较低。故需要采取各种措施改善。除了采取弹性模量小、热膨胀系数低的材料外,结构上也有很多措施,比如两端附加刚度低的波纹管段,采取断开式或悬臂结构等,这样测量管就可简化为不同支承的梁。
下面我们就分析几种支承对于模态频率的影响。分析测量管的模态,分析方法同前,长度396mm,壁厚lmm,支承状态及响应的模态频率(单位为Hz)如表2所示。
表2 支承类型对模态频率的影响
| 支承 | |||||
| 阶次 | 两端固支 | 一端固支 一端轴向自由 | 两端轴向自由 | 自由状态 | 悬臂状态 |
| 一阶(弯曲) | 446.52 | 308.321 | 197.533 | 446.755 | 70.6445 |
| 二阶(弯曲) | 1215.16 | 989.764 | 785.203 | 1221.35 | 439.713 |
| 三阶(弯曲) | 2344.22 | 2038.01 | 1748.84 | 2366.12 | 1218.78 |
| 四阶(弯曲) | 3801.64 | 3201.97(收缩) | 3066.7 | 3852.21 | 2355.05 |
比较表2不同支承的模态频率,可以知道,两端固支(限制节点的所有自由度)和不约束时,模态相同,模态频率较高。
轴向可以自由伸缩时,一价模态频率降低,仅一端轴向自由(约束除轴向外的其余自由度)时,模态频率居中;两端均轴向白由时,模态频率更低一些,一端完全自由的(悬臂),一阶模态频率最低。
有自由端时,模态频率降低的原因,应该主要是弯曲过程中基本消除了轴向伸缩振动产生的轴向力的影响。实际振动中,由于轴向伸缩振动过程中存在惯性力,所以轴向力不可能完全消除。当有一端固定的时候,会对轴向伸缩振动产生约束,会增大轴向力,所以会增大模态频率。
一端固定,另一端可自由伸缩时,其结果相对两端全部固定的测量管模态频率低,由于约束不对称,出现了模态的不对称,而且由于轴向自由度没有限制出现轴向收缩模态(限于篇幅,图略去)。
5 结论
有限元分析在科里奥斯质量流量计的动态分析中有重要作用,本文对其进行了模态分析计算。对于整体的模态分析,依据其轴对称结构特点,可利用现成的二维CAD视图,导人到Marc中,对不同的零件区域分别划分网格,然后旋转生成三维模型。采用Lanczos法计算模态。对比单独的测量管模型的模态计算结果,可知整体模型的模态类型多,可能有一些模态会干扰测量管的正常工作模态。另外支承状态对模态有很大影响,主要原因是弯曲振动引起的附加轴向伸缩振动,产生的轴向力会阻碍弯曲振动。参考文献
l 张世基振动学基础。北京:北京航空航天大学出版社,1990
2 仝猛,任萍,陈明 Coriolis质量流量计中的相位差检测方法研究。测控技术,2001(1)
3 仝猛,任萍,陈明。单直管科氏质量流量计结构研究。航空计测技术,2000,20(4):7~9
---------------------------------
收稿日期:2002一12一25。
第一作者仝猛,男,1970年生,在读博士研究生;研究领域:精密仪器及精密加工、新型传感器理论和应用、微弱信号检测技术、振动理论等,已发表论文10余篇。


 推荐产品
推荐产品


 相关视频
相关视频