雷诺数和节流装置的计算

雷诺数

当导出流量基本方程式(1，34)及(1，35)时，为了简化，会假定在导管截面全速度分布为不变的。

其实，在导管截面上速度的分布是变化的。这是由于流体对管壁的摩擦以及以不同速度流过的流体质点间的摩擦所引起的。

假定在容器中的粘滞流体（图10）是静止的，而在其中移动一平板（平壁）。当平板移动时，流体质点亦为其所带引，并且在平板旁之流体层以平板之速度移动。距平板越远，则被带引之流体层的速度越小。速度的减小实际上是直线进行的。

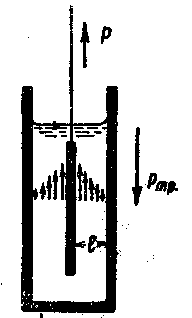图10粘滞力示意图

令流体中平板以速度W移动时，必须向其施以力P。此力正比于平板的移动速度，因而

            P=rW.                                (1，51)

摩擦系数r 决定于接触面积F、平板与器壁间流体层的厚度 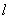以及流体的性质，亦即粘度系数 。

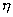           r= 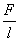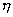,                              (1, 52)

而摩擦力按下式确定：

          P_rp= 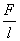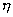W,                           （1，53）

粘度等于在速度变化 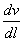=1时相互作用的某一流体层单位表面积从另一流体层（或平壁）方面所受的力。粘度的工程单位为下述物质的粘度，在这种物质中，当相距1[公尺]的速度梯度等于1[公尺/秒]时，每[公尺²]流体层表面积上有1[公斤]的摩擦力作用。换言之，两个相距1[公尺]、面积为1[公尺²]流体层当以相对速度1[公尺/秒]移动时，相互作用的力取为粘度的工程单位。粘度的工程单位的因次为[公斤][秒]/[公尺]²。

当平板移动速度不大时，被它所带引的流体质点平行地移动，此即为层流。若增大速度，则惯性力迅速增加，因为惯性力与速度是成平方关系的：

         Pn= 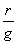W²F。                          （1，54）

惯性力与摩擦力有一临界比例，此时仅与速度成一次幂关系的摩擦力与惯性相比失去意义。流体质点逐作无规则的移动，即在流体的边界层中发生湍流。

如此，可按照惯性力与摩擦力之比来判断流束的特性。

惯性力与摩擦力之比称为雷诺数：

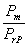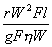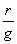
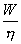
       Re= = =      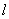                (1,55)

为了简化起见，在方程式（1，55）中以动粘度v替动力粘度 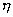。动粘度为液体或气体的粘度与密度之比v= 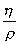,或

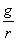
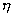         v= 。                                 （1，56）

则雷诺数式有下面的形式：

            Re= 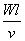                                      (1, 57)

式中 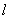为流束之任一直线尺寸，如孔板之孔径Red或导管的直径Red。我们随后将对导管的内径来表示雷诺数。

             ReD= 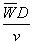。                               （1，58）

如此，任一流体之流动特性取决于三个数量：平均速度、流束的几何尺寸以及操作状态下流动介质的动粘度。

层流转为湍流发生于约等于2300的所谓临界雷诺数时。

            Re_DKP≈2300

低于此数，由于摩擦力对惯性力占优势，涡漩消失，流束互相平行，并与导管中心线平行，流束平稳，转为在流束横截面上具有抛物线的速度颂特性之层流。最大速度在导管中心线上，至管壁则等于零。

高于此临界雷诺数时，惯性力占优势，遂发生由于各个流束的不规则的横向流动所引起之涡漩。流束横向涡漩之发生是由于在中心线附近流速较大。在该处由于动能增大而静压力减小。在流束的横流束横向涡漩之发生是由于在中心线附近流速较大。在该处由于动能增大面静压力减小。在流束的横截方向上产生压降，因而外面的与中心的流束互相搅混，就成为湍流。剧烈的横向流动使速度的抛物线发生畸变。沿横截面的速度分布变得较均匀；自管壁开始速度突增，并在流束横截面之其余几乎保持不变。

在临界雷诺数附近之湍流区域内也可能为层流，但不稳定；稍加扰动即转为湍流。由此而雷诺数的临界值附近有一流束不稳定（过渡）区域。

雷诺数表明粘滞流体流束的流体动力相似定律。这可以这样来说明：粘滞流体的两个几何动，只当其雷诺数相等时具有相同的流动动力条件：

               Re^I=Re2=… 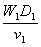= =…             （1，59）

当两个流束之间具有几何相似及动力相似时，即两个几何相似的流束的雷诺数相等时，则此二流束之流量系数亦相等。

相似定律使得我们可以将对某些尺寸的节流装置所得之实验数据的结果运用于其他密度和粘度的物质上，也可运用于与之几何相似的其他尺寸的节流装置上。