 文章内容
文章内容
容积式流量计的误差特性
对于任何一个流量测量值来说,必须包括两部分内容:一是流量测量值本身;二是它的误差允许范围.否则是不完整的.所以,对于任何一种流量计,都必须了解它的误差特性。
所谓误差特性,就是流量计的误差值与流量测量值之间的关系。讨论误差特性,就是讨论和研究测量误差值随流量测量值变化而变化的趋势.
容积式流量计的测量误差值E,可由指示值与真值之差与指示值之比表示.设:V为通过流量计的流体体积真值;I为流量计指示值,则误差值E可表示为
E= 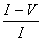 (2-5)
(2-5)
将流体体积V与指示值I之间的关系式(2-3)代入,可得:
E=1- 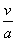 (2-6)
(2-6)
由式2-6可见,容积式流量计的误差特性仅与流量计内部的计量空间体积v、仪表齿轮比常数a有关.也就是说,从测量原理的角度来说,容积式流量计的测量误差仅与流量计的几何结构有关,而与流体性质和流量值无关,我们把这个误差特性称为容积式流量计的理想误差特性.画成曲线,是一条平行于横轴的水平线,如图2-6中曲线1所示.
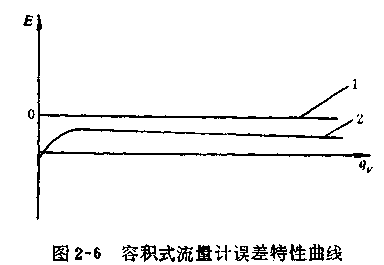
然而,当我们对容积式流量计进行标定,画出实际误差特性曲线时,则较接近曲线2的形式.在小流量时,误差值急剧地向负方向倾斜;随着流量增大,误差值逐渐由负方向向正方向移动,并稳定在某一定位上,误差曲线平行于横轴.流量继续增加,误差值又将向负方向偏移.实际误差特性曲线所以呈现这种变化趋势,是因为在于容积式流量计中存在着不可避免的漏流现象.所谓漏流,就是流体通过转动件与外壳之间的间隙直接从入口流向出口,没有被计量.以下将讨论考虑了漏流现象的误差特性关系式.
假设在单位时间内的流体漏流量用 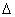 g表示;通过流量计的流量为qv;通过流量计总的流体体积量为V;在这一段时间内总的漏流的体积量为
g表示;通过流量计的流量为qv;通过流量计总的流体体积量为V;在这一段时间内总的漏流的体积量为 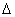 V.这株
V.这株 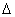 V可表示为
V可表示为
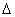 V=
V= 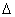 g
g  (2-7)
(2-7)
所以,当存在漏流时,转子排出N个计量空间流体量时,实际通过流量计的流体体积为
V=Nv+ 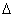 V
(2-8)
V
(2-8)
将式2-2,2-7代入式2-8,可得:
V=  v+
v+ 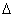 g
g  (2-9)
(2-9)
式(2-9)可整理成:
V= 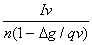 (2-10)
(2-10)
将式(2-10)代入误差定义式(2-5),可得:
E=1-  (2-11)
(2-11)
分析式2—11可见,由于计量空间体积v、齿轮比常数a均为定值,所以误差E与流量之间的关系受单位时间漏流量 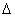 g影响.
g影响.
若假定该容积式流量计的漏流量  g是一恒定值,可利用式(2—11)讨论其误差曲线的变化趋势.
g是一恒定值,可利用式(2—11)讨论其误差曲线的变化趋势.
当流量很小,在极端情况下,qr=  g,则式(2—11)中括号内为0,误差值E趋向负无穷大.
g,则式(2—11)中括号内为0,误差值E趋向负无穷大.
随着流量qv增加,式(2—11)中括号内数值逐渐增大,误差值E也逐渐向正方向增加。
当流量继续增加,达到  g与qv相比显得非常小,即
g与qv相比显得非常小,即  g/qv很接近0时,式(2—11)转变成式(2-6),误差曲线趋向于理想误差曲线.
g/qv很接近0时,式(2—11)转变成式(2-6),误差曲线趋向于理想误差曲线.


 推荐产品
推荐产品


 相关视频
相关视频