涡街流量计的原理

 

    1．卡门涡街的产生与现象

    为说明卡门涡街的产生，我们来考虑粘性流体绕流圆柱体的流动．当流体速度很低时，流体在前驻点速度为零，来流沿圆柱左右两侧流动，在圆柱体前半部分速度逐渐增大，压力下降，后半部分速度下降，压力升高，在后驻点速度又为零．这时的流动与理想流体统流圆柱体相同，无旋涡产生，如图3—7a所示．

    随着来流速度增加，圆柱体后半部分的压力梯度增大，引起流体附面层的分离，如图3—7b所示．当来流的雷诺数Re再增大，达到40左右时，由于圆柱体后半部附面层中的流体微团受到更大的阻滞，就在附面层的分离点S处产生一对旋转方面相反的对称旋涡．如图3－7c所示．

在一定的留诺数Re范围内，稳定的卡门涡街的及旋涡脱落频率与流体流速成正比．

图3－7   圆柱绕涡街产生示意图

2．卡门涡街的稳定条件

并非在任何条件下产生的涡街都是稳定的．冯·卡门在理论上已证明稳定的涡街条件是：涡街两列旋涡之间的距离为h，单列两涡之间距离为 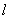，若两者之间关系满足

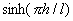                         ＝1

              或                  h / 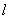＝0. 281                     （3－24）

时所产生的涡街是稳定的。

    3．涡街运动速度

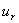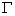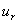为了导出旋涡脱落频率与流速之间的关系，首先要得到涡街本身的运动速度 ．为便于讨论，我们假定在旋涡发生体上游的来源是无旋、稳定的流动，即其速度环量为零．从汤姆生定理可知，在旋涡发生体下游所产生的两列对应旋涡的速度环量 ，必然大小相等，方向相反，其合环量为零，由于对应两涡的旋向相反，速度环量大小相等，所以在整个涡群的相互作用下，涡街将以一个稳定的速度 向上游运动．从理论计算可得． 的表示式为

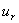              ＝ tan h                                 (3-25)

对于稳定的涡街，将式（3－25）代入，有：

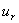            = tan h(0. 281 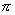)=                        (3-26)

4．流体流速与旋涡脱落频率的关系

    从前面讨论可知，当流体以流速u流动时，相对于旋涡发生体，涡街的实际向下游运动速度为u－ur．如果单列旋涡的产生频率为每秒f个旋涡，那么，流速与频率的关系为

                       u－ur = fl                        (3－27)

    将式(3－26)代入，可得到流速u与旋涡脱落频率f之间的关系．但是，在实际上不可能测得速度环量 的数值，所以只能通过实验来确定来流速度u与涡街上行速度ur之间的关系，确定因注形旋涡发生体直径d与涡街宽度h之间的关系，有：

h＝1. 3d                        （3－28）

ur＝0. 14u                       （3－29）

将式（3－24），（3－27），（3－28），（3－29）联立，可得：

                  f＝ ＝ ＝        （3－29’）

                  0. 2u / d

也可将上式写成：

                  St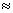＝ 0. 2                        (3－30)

St称为斯特罗哈数．从实验可知，在雷诺数Re为3×l0²－3×l0⁵范围内，流体速度u与旋涡脱落频率的关系是确定的．也就是说，对于圆柱形旋涡发生体，在这个范围内它的斯特罗哈数St是常数，并约等于0．2，与理论计算值吻合的很好．对于圆柱型式的旋涡发生体，其斯特罗哈数St也是常数，但有它自己的数值．图3－8为圆往型旋涡发生体产生的涡街结构．

根据以上分析，从流体力学的角度可以判定涡街流量计测量的上下限流量为：Re＝3×10²－2×l0⁵．当雷诺数更大时，圆柱体周围的边界层将变成紊流，不符合上述规律，并且将会是不稳定的．

图3－8     涡街结构示意图

5．流体振动原理

    当涡街在旋涡发生体下游形成以后，仔细观察其运动，可见它一面以速度u－ur平行于轴线运动，另外还在与轴线垂直方向上振动．这说明流体在产生旋涡的同时还受到一个垂直方向上力的作用．下面讨论这个垂直方向上力的产生原因及计算方法．

同前讨论，假定来流是无旋的，根据汤姆生定律：沿封闭流动流线的环量不随时间而改变．那么，当在旋涡发生体右(或左)下方产生一个旋涡以后，必须在其它地方产生一个相反的环量，以使合环量为零．这个环量就是旋涡发生体周围的环流．根据茹科夫斯基的升力定理，由于这个环量的存在，会在旋涡发生体上产生一个升力，该升力垂直于来流方向．设作用在旋涡发生体每单位长度上的升力为L，有：

                 L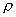＝ u 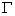                            （3－31）

式中 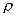  ――流体密度；

        u――来流速度；

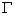――旋涡发生体的速度环量．

    从前面的讨论中可以得到以下关系，

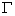  ＝2 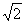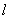ur；ur=K1u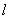； ＝K2d ；

    将上述关系代入式(3—1)，并令系数K＝2 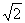K1K2，则有：

                    L＝K 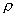du²                             (3－32)

    这就是作用在旋涡发生体上的升力．由于旋涡在旋涡发生体两侧交替发生，且旋转方向相反，故作用在发生体上的力亦是交替变化的．而流体则受到发生体的反作用力，产生垂直于铀线方向的振动，这就是流体振动的原理．

    从上述分析可以知道：交替地作用在旋涡发生体上升力的频率就是旋涡的脱落频率．通过检测该升力的变化频率，就可以得到旋涡的脱落频率，从而可得流体的流速值。

    6．流量公式

涡街流量计是一种速度式流量计，它测的是流体的流速u．为得到流量值，必须乘以流通截面积A．对于不同形式的旋涡发生器，它的流通截面积计算是不同的．以下仅举圆柱形流通截面积A可表示为

                  A≈ 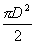（1－1. 25 ）                     （3－33）

由此可得流量公式为

                 qv＝Au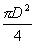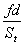＝ （1－1. 25 ）             （3－34）

从该式可知，流量qv与旋涡脱落频率f在一定雷诺数范围内成线性关系。因此，也将这种流量计称为线性流量计。