推荐产品
相关视频
文章内容
基于声学法的炉膛二维温度场图像重建(2)
（2）2004年9月
这样，便求出了每一分割区域的空间特性，即声波在该区域传播时声速的倒数。利用(1)式可求出各区域的平均温度，即
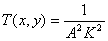
将各区域平均温度作为区域几何中心点的温度，利用插值算法便可拟合出整个待测二维温度场。
2 基于费马定理对声波路径弯曲效应实现补偿的炉内温度分布重建
声波路径的弯曲效应是指声波从发射器到接收器的路径不一定是两传感器之间的直线段，而可能是两传感器之间的一条曲线。根据费马定理，在多相介质中，射线沿两点间传播时间最短的路径前近[5]，而工业炉内的温度场为非均温场，这必然使得声波路径要弯向温度较高的地方，即发生了声波路径的弯曲效应。在上述的温度场重建过程中，我们将声波路径的弯曲效应。在上述的温度场重建过程中，我们将声波路径假设为两传感器之间的直线段，从而给重建结果带来较大的误差，因此必须对声波路径弯曲效应进行补偿。
第K条声波路径可表示成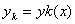 
，沿着这条路径长度S的微分可写成
（7）
因此，声波从反射位置（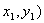 
到接收位置（ 
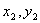）的飞行时间为
（8）
根据费马定理，时间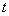 
必取极小值，因为 
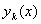为声波路径。根据欧拉方程可得[6]
= 
首先，将声波传播路径按直线处理重建温度场T（x,y），然后利用打靶法解方程组（9），取得声波弯曲路径上的一系列点的位置坐标，修正方程（5）中的矩阵S[7]，重建声波路径弯曲情况下的温度场。
为验证上述算法对不同温度分布的重建效果，本文对不同温度分布模型在80×80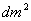 
的典型层面进行了仿真研究，温度场模型的具体形式为[5]
（10）
式中： 
为线性系数（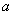 
的选取取决于期望温度场的平均温度分布，b的选取取决于期望的温度梯度）； 
、 
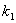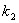为常数；（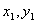 
）为火焰峰值的位置。
3.2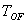 
数据的获取
由温度场函数（仿真数学模型）和传感器位置计算声音的传播路径；再由式（11）计算声波的飞行时间
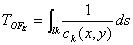（11）
式中：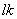 
为第K条声音传播路径；T 
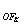为声波K条传播路径的飞行时间； 
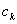为声音传播速度，它是温度的函数。
3.3 重建图象质量的评价
在对工业炉二维温度场重建进行仿真结果分析时，采用最大相对误差、均方根误差为重建图像的质量系数[8]。其中，均方根误差的定义为
（12）
